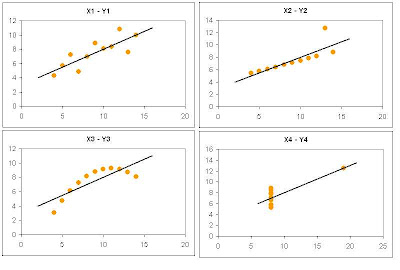
Las 4 variables Y tienen la misma media y desviación estándar. Además el coeficiente de correlación entre X e Y es el mismo en los 4 casos (0.816) y comparten la misma recta de regresión y = 0.5 x + 3Las cuatro relaciones con distintas entre si, pero sus correlaciones son las mismas. Esto nos enseña la importancia de usar gráficos de dispersión para visualizar la relación entre dos variables, más que confiar en su correlación.
¿Pero qué sucede si analizamos estas relaciones usando medidas de información?
La primera diferencia que encontramos es que las entropías de las variables Y son distintas, excepto las dos últimas. La diferencia más importante es que la información transmitida entre cada par de valores es diferente en los 4 casos, como puede verse en la siguiente tabla
En los tres primeros casos, la información transmitida nos indica que es posible realizar un buen modelo, mientras que en el último caso, un valor de sólo 18% nos dice que ningún modelo será capaz de hacer un buen trabajo para representar esta relación (lo cual es obvio mirando el gráfico de dispersión).
La información transmitida no asume ningún tipo de relación, como lo hace el coeficiente de correlación. Esta es una gran ventaja, porque muchos data sets contienen relaciones no-lineales que son descartadas al utilizar correlaciones lineales.
En casos que involucran sólo dos variables, una manera de confirmar si la relación es lineal es usar los gráficos de dispersión, pero cuando aparecen más variables independientes, graficar la relación no sirve. Una solución es utilizar medidas de información mutua como la información transmitida.
